Behavior nodes provide the means for animating objects, processing keyboard and mouse inputs, reacting to movement, and enabling and processing pick events. Behavior nodes contain Java code and state variables. A Behavior node's Java code can interact with Java objects, change node values within a Java 3D scene graph, change the behavior's internal state-in general, perform any computation it wishes.
Simple behaviors can add surprisingly interesting effects to a scene graph. For example, one can animate a rigid object by using a Behavior node to repetitively modify the TransformGroup node that points to the object one wishes to animate. Alternatively, a Behavior node can track the current position of a mouse and modify portions of the scene graph in response.
A Behavior leaf node object contains a scheduling region and two
methods: an initialize method called once when the
behavior becomes "live" and a processStimulus
method called whenever appropriate by the Java 3D behavior
scheduler.
The Behavior object also contains the state information needed by its initialize
and processStimulus methods.
The scheduling region defines a spatial volume that serves to enable the scheduling of Behavior nodes. A Behavior node is active (can receive stimuli) whenever an active ViewPlatform's activation volume intersects a Behavior object's scheduling region. Only active behaviors can receive stimuli.
The scheduling interval defines a partial order of execution for behaviors that wake up in response to the same wakeup condition (that is, those behaviors that are processed at the same "time"). Given a set of behaviors whose wakeup conditions are satisfied at the same time, the behavior scheduler will execute all behaviors in a lower scheduling interval before executing any behavior in a higher scheduling interval. Within a scheduling interval, behaviors can be executed in any order, or in parallel. Note that this partial ordering is only guaranteed for those behaviors that wake up at the same time in response to the same wakeup condition, for example, the set of behaviors that wake up every frame in response to a WakeupOnElapsedFrames(0) wakeup condition.
The processStimulus method receives and processes a
behavior's ongoing messages. The Java 3D behavior scheduler
invokes a
Behavior node's processStimulus
method when an active ViewPlatform's activation volume intersects a
Behavior object's scheduling region and all of that behavior's wakeup
criteria are satisfied. The processStimulus method
performs its computations and actions (possibly including the
registration of state change information that could cause Java 3D
to
wake other Behavior objects), establishes its next wakeup condition,
and finally exits.
A typical behavior will modify one or more nodes or node components in the scene graph. These modifications can happen in parallel with rendering. In general, applications cannot count on behavior execution being synchronized with rendering. There are two exceptions to this general rule:
processStimulus
method of a single behavior instance are guaranteed to take effect in
the same rendering frameprocessStimulus
methods of the set of behaviors that wake up in response to a
WakeupOnElapsedFrames(0) wakeup condition are guaranteed to take effect
in the same rendering frame.Note that modifications to geometry by-reference or texture by-reference are not guaranteed to show up in the same frame as other scene graph changes.
When the Java 3D behavior scheduler invokes a Behavior object's
processStimulus
method, that method may perform any computation it wishes. Usually, it
will change its internal state and specify its new wakeup conditions.
Most probably, it will manipulate scene graph elements. However, the
behavior code can change only those aspects of a scene graph element
permitted by the capabilities associated with that scene graph element.
A scene graph's capabilities restrict behavioral manipulation to those
manipulations explicitly allowed.
The application must provide the Behavior object with references to
those scene graph elements that the Behavior object will manipulate.
The application provides those references as arguments to the
behavior's constructor when it creates the Behavior object.
Alternatively, the Behavior object itself can obtain access to the
relevant scene graph elements either when Java 3D invokes its initialize
method or each time Java 3D invokes its processStimulus
method.
Behavior methods have a very rigid structure. Java 3D assumes that they always run to completion (if needed, they can spawn threads). Each method's basic structure consists of the following:
A WakeupCondition object is an abstract class specialized to fourteen different WakeupCriterion objects and to four combining objects containing multiple WakeupCriterion objects.
A Behavior node provides the Java 3D behavior scheduler with a WakeupCondition object. When that object's WakeupCondition has been satisfied, the behavior scheduler hands that same WakeupCondition back to the Behavior via an enumeration.
Java 3D provides a rich set of wakeup criteria that Behavior
objects
can use in specifying a complex WakeupCondition. These wakeup criteria
can cause Java 3D's behavior scheduler to invoke a behavior's processStimulus
method whenever
A Behavior object constructs a WakeupCriterion by constructing the appropriate criterion object. The Behavior object must provide the appropriate arguments (usually a reference to some scene graph object and possibly a region of interest). Thus, to specify a WakeupOnViewPlatformEntry, a behavior would specify the region that will cause the behavior to execute if an active ViewPlatform enters it.
A Behavior object can combine multiple WakeupCriterion objects into a more powerful, composite WakeupCondition. Java 3D behaviors construct a composite WakeupCondition in one of the following ways:
WakeupCriterion && WakeupCriterion && ...
WakeupCriterion || WakeupCriterion || ...
WakeupOr && WakeupOr && ...
WakeupAnd || WakeupAnd || ...
Behavior objects can condition themselves to awaken only when signaled by another Behavior node. The WakeupOnBehaviorPost WakeupCriterion takes as arguments a reference to a Behavior node and an integer. These two arguments allow a behavior to limit its wakeup criterion to a specific post by a specific behavior.
The WakeupOnBehaviorPost WakeupCriterion permits behaviors to chain their computations, allowing parenthetical computations-one behavior opens a door and the second closes the same door, or one behavior highlights an object and the second unhighlights the same object.
As a virtual universe grows large, Java 3D must carefully husband its resources to ensure adequate performance. In a 10,000-object virtual universe with 400 or so Behavior nodes, a naive implementation of Java 3D could easily end up consuming the majority of its compute cycles in executing the behaviors associated with the 400 Behavior objects before it draws a frame. In such a situation, the frame rate could easily drop to unacceptable levels.
Behavior objects are usually associated with geometric objects in the virtual universe. In our example of 400 Behavior objects scattered throughout a 10,000-object virtual universe, only a few of these associated geometric objects would be visible at a given time. A sizable fraction of the Behavior nodes-those associated with nonvisible objects-need not be executed. Only those relatively few Behavior objects that are associated with visible objects must be executed.
Java 3D mitigates the problem of a large number of Behavior nodes in a high-population virtual universe through execution culling-choosing to invoke only those behaviors that have high relevance.
Java 3D requires each behavior to have a scheduling region and to post a wakeup condition. Together a behavior's scheduling region and wakeup condition provide Java 3D's behavior scheduler with sufficient domain knowledge to selectively prune behavior invocations and invoke only those behaviors that absolutely need to be executed.
Java 3D finds all scheduling regions associated with Behavior nodes and constructs a scheduling/volume tree. It also creates an AND/OR tree containing all the Behavior node wakeup criteria. These two data structures provide the domain knowledge Java 3D needs to prune unneeded behavior execution (to perform "execution triage").
Java 3D must track a behavior's wakeup conditions only if an active ViewPlatform object's activation volume intersects with that Behavior object's scheduling region. If the ViewPlatform object's activation volume does not intersect with a behavior's scheduling region, Java 3D can safely ignore that behavior's wakeup criteria.
In essence, the Java 3D scheduler performs the following checks:
true,
schedule that Behavior object for execution.Java 3D's behavior scheduler executes those Behavior objects
that
have
been scheduled by calling the behavior's processStimulus
method.
This section describes Java 3D's predefined Interpolator behaviors. They are called interpolators because they smoothly interpolate between the two extreme values that an interpolator can produce. Interpolators perform simple behavioral acts, yet they provide broad functionality.
The Java 3D API provides interpolators for a number of functions: manipulating transforms within a TransformGroup, modifying the values of a Switch node, and modifying Material attributes such as color and transparency.
These predefined Interpolator behaviors share the same mechanism for specifying and later for converting a temporal value into an alpha value. Interpolators consist of two portions: a generic portion that all interpolators share and a domain-specific portion.
The generic portion maps time in milliseconds onto a value in the range [0.0, 1.0] inclusive. The domain-specific portion maps an alpha value in the range [0.0, 1.0] onto a value appropriate to the predefined behavior's range of outputs. An alpha value of 0.0 generates an interpolator's minimum value, an alpha value of 1.0 generates an interpolator's maximum value, and an alpha value somewhere in between generates a value proportionally in between the minimum and maximum values.
Several parameters control the mapping of time onto an alpha value (see the javadoc for the Alpha object for a description of the API). That mapping is deterministic as long as its parameters do not change. Thus, two different interpolators with the same parameters will generate the same alpha value given the same time value. This means that two interpolators that do not communicate can still precisely coordinate their activities, even if they reside in different threads or even different processors-as long as those processors have consistent clocks.
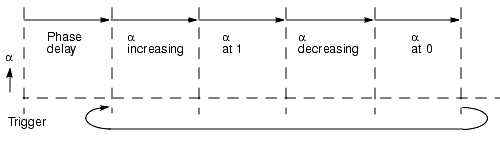
Figure 1 shows the components of an interpolator's time-to-alpha mapping. Time is represented on the horizontal axis. Alpha is represented on the vertical axis. As we move from left to right, we see the alpha value start at 0.0, rise to 1.0, and then decline back to 0.0 on the right-hand side.
On the left-hand side, the trigger time defines when this interpolator's waveform begins in milliseconds. The region directly to the right of the trigger time, labeled Phase Delay, defines a time period where the waveform does not change. During phase delays alpha is either 0 or 1, depending on which region it precedes.
Phase delays provide an important means for offsetting multiple interpolators from one another, especially where the interpolators have all the same parameters. The next four regions, labeled α increasing, α at 1, α decreasing, and α at 0, all specify durations for the corresponding values of alpha.
Interpolators have a loop count that determines how many times to repeat the sequence of alpha increasing, alpha at 1, alpha decreasing, and alpha at 0; they also have associated mode flags that enable either the increasing or decreasing portions, or both, of the waveform.
Developers can use the loop count in conjunction with the mode flags to generate various kinds of actions. Specifying a loop count of 1 and enabling the mode flag for only the alpha-increasing and alpha-at-1 portion of the waveform, we would get the waveform shown in Figure 2.
In Figure 2, the alpha value is 0 before the combination of trigger time plus the phase delay duration. The alpha value changes from 0 to 1 over a specified interval of time, and thereafter the alpha value remains 1 (subject to the reprogramming of the interpolator's parameters). A possible use of a single alpha-increasing value might be to combine it with a rotation interpolator to program a door opening.
Similarly, by specifying a loop count of 1 and a mode flag that enables only the alpha-decreasing and alpha-at-0 portion of the waveform, we would get the waveform shown in Figure 3.
In Figure 3, the alpha value is 1 before the combination of trigger time plus the phase delay duration. The alpha value changes from 1 to 0 over a specified interval; thereafter the alpha value remains 0 (subject to the reprogramming of the interpolator's parameters). A possible use of a single α-decreasing value might be to combine it with a rotation interpolator to program a door closing.
We can combine both of the above waveforms by specifying a loop count of 1 and setting the mode flag to enable both the alpha-increasing and alpha-at-1 portion of the waveform as well as the alpha-decreasing and alpha-at-0 portion of the waveform. This combination would result in the waveform shown in Figure 4.
In Figure 4, the alpha value is 0 before the combination of trigger time plus the phase delay duration. The alpha value changes from 0 to 1 over a specified period of time, remains at 1 for another specified period of time, then changes from 1 to 0 over a third specified period of time; thereafter the alpha value remains 0 (subject to the reprogramming of the interpolator's parameters). A possible use of an alpha-increasing value followed by an alpha-decreasing value might be to combine it with a rotation interpolator to program a door swinging open and then closing.
By increasing the loop count, we can get repetitive behavior, such as a door swinging open and closed some number of times. At the extreme, we can specify a loop count of -1 (representing infinity).
We can construct looped versions of the waveforms shown in Figure 2, Figure 3, and Figure 4. Figure 5 shows a looping interpolator with mode flags set to enable only the alpha-increasing and alpha-at-1 portion of the waveform.
In Figure 5, alpha goes from 0 to 1 over a fixed duration of time, stays at 1 for another fixed duration of time, and then repeats.
Similarly, Figure 6 shows a looping interpolator with mode flags set to enable only the alpha-decreasing and alpha-at-0 portion of the waveform.
Finally, Figure 7 shows a looping interpolator with both the increasing and decreasing portions of the waveform enabled.
In all three cases shown by Figure 5, Figure 6, and Figure 7, we can compute the exact value of alpha at any point in time.
Java 3D's preprogrammed behaviors permit other behaviors to change their parameters. When such a change occurs, the alpha value changes to match the state of the newly parameterized interpolator.
Commonly, developers want alpha to change slowly at first and then
to
speed up until the change in alpha reaches some appropriate rate. This
is analogous to accelerating your car up to the speed limit-it does not
start off immediately at the speed limit. Developers specify this
"ease-in, ease-out" behavior through two additional parameters, the increasingAlphaRampDuration
and the decreasing-AlphaRampDuration.
Each of these parameters specifies a period within the increasing or
decreasing alpha duration region during which the "change in alpha" is
accelerated (until it reaches its maximum per-unit-of-time step size)
and then symmetrically decelerated. Figure
8 shows three general examples of how the increasingAlphaRampDuration
method can be used to modify the alpha waveform. A value of 0 for the
increasing ramp duration implies that α
is not accelerated; it changes at a constant rate. A value of 0.5 or
greater (clamped to 0.5) for this increasing ramp duration implies that
the change in α is accelerated during the first half of the
period and
then decelerated during the second half of the period. For a value of n
that is less than 0.5, alpha is accelerated for duration n,
held constant for duration (1.0 - 2n), then decelerated for
duration n of the period.